SCMP 391 – Lab 8

Enhanced Microcoded Operations

Goal

To create and test a system that allows looping and branching within the micro-program.

Introduction

The big problem with the machine we ended with in Lab 7 is that the microprogram cannot make decisions about what to do next. It can only do the sequence of instructions that are in the ROM. How can we do this? Notice we left quite a few bits undefined. What we can do is put an 8-bit ROM address in bits 24-31 of the micro instruction. This will be the address of the next instruction in the microcode if a branch is to occur. So now we can either go to the next instruction, or use the branch address to branch somewhere else.

So – how do we determine when to branch? Typically there will be some type of BRANCH CONDITION that we will sense. For example, we can use the ALU N or the Z bits to signal for a branch. Below we see a such a circuit. When N and Z bits are are both zero in the micro-instruction, the next ROM address will be taken from the MPC (the Micro Program Counter). However, when either the N or Z (or both) are set in them microinstruction, AND when the corresponding ALU (Z or N) bit is true, then the next ROM address will taken from the address embedded in the current microinstruction.

What if we want an unconditional branch? Then we can add another bit to the microinstruction that will signal that a branch is always to occur.

Step 1 – The microsequencer

Below is a completed microsequencer for the system we are building. Carefully go through its functionality. When you believe you understand it, build and test it.

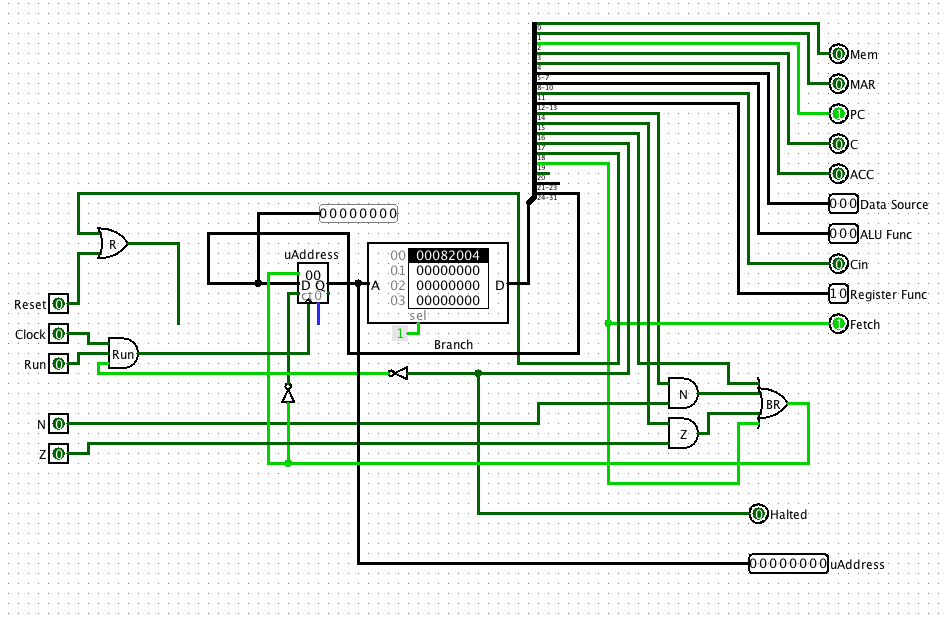
Some points to note:

1. The reset is asynchronous. Thus if you set the reset bit in an instruction it immediately goes to location zero, the rest of the instructions in the microinstruction are ignored.
2. The Branch signal is 1 when we want to increment, a 0 when we want to go to the next instruction. So we put it directly to the Load input of the counter, and through a NOT gate to the count input. This way we get a increment when went branch is zero, and a load when branch is one.

Lets test the microsequencer!

To Do

1. Looking at the sequencer above, put a 4000 in uCode[0x2]. This is the branch on N instruction. Set N to zero. Reset the sequencer (set reset to 1, then back to zero), and step through the memory by clicking the clock on and off (with Run set to 1). What happens?
2. Now set N to 1. Reset and try again. What happened now?
3. Now try with uCode[0x2] set to 00008000, and then try with 00010000. What is each of these instructions? When does branching occur for each?
4. Finnally try with uCode[0x2] set to 0000c000. What does this instruction do? Is this useful?
5. Take a screenshot of your circuit, and include in your lab report.

Step 2 – The complete system

Below is the definition for the microprogram control words:

Branch Address	Unused	Reset	Halt	Uncond Branch	Z	N	Reg Func	Cin	ALU Func	Data Source	ACC	C	B	MAR	Mem
31-24	23-19	18	17	16	15	14	12-13	11	8-10	5-7	4	3	2	1	0
0xFF000000		0x40000	0x20000	0x10000	0x8000	0x4000	0x3000	0x800	0x700	0xE0	0x10	0x8	0x4	0x2	0x1

The bit fields are defined as follows:

ALU Functions

Bits	Operation
000	ACC
001	Reg
010	ACC’
011	Reg ^ ACC
100	Reg V ACC
101	Reg + ACC + Cin
110	-Reg
111	ACC-Reg

Data Source

Bits	Source
000	Input
001	Memory
010	MAR
011	B
100	C
101	ACC

What remains to be done? Connect the sequencer as a subcircuit with the larger system.

Programming with loops

First, let’s write a program that computes M[2]=M[0] x M[1]. Values are unsigned numbers. What we will do is add M[1] to itself M[0] times. Here is an algorithm:

        ACC,MAR <- 0            // Clear ACC and MAR
        B <- Mem[MAR]           // Get first value
        MAR++                   // Go to next (M[1])
        C <- Mem[MAR]           // Get second value
loop:   If B == 0 goto end      // If number of additions left is zero, end
        ACC = ACC + C           // Add second value to ACC
        B--                     // count this add
        goto loop               // repeat     
end:    MAR++                   // Go to M[2]
        Mem[MAR] <- ACC         // put result in place
        halt                    // doneCode language: PHP (php)

Here is a micro-program:

Operation	Address	Instruction	Comment
ACC,MAR <- 0	0	1012	Clear ACC and MAR. ACC will be our partial sum.
B <- Mem[MAR]	1	124	Put Mem[0] into B.
MAR++	2	2002	Point to Mem[1]
C <- Mem[MAR]	3	128	Put Mem[1] into C
If B == 0 goto 8	4	8008160	If B is zero, we are done
ACC = ACC + C	5	590
B–	6	3004	Count this loop
goto 4	7	4010000	Go add again
MAR++	8	2002	Advance MAR to Mem[2]
Mem[MAR] <- ACC	9	1a1	Put result in Mem[2]
halt	10	20000	Done

Program:

v2.0 raw
1012 124 2002 128 8008160 590 3004 4010000 
2002 1a1 20000

As you can see here we can now produce a microprogram that will compute some specific function. It’s still limited but has some function.

Before we program it, you will be happy to know there is an updated microprogram instruction generator for this machine all ready to use: Microcode Generator 2

To Do

1. Get the machine above fully working
2. Take a screenshot and put it in your lab report.
3. Write a microprogram that will sum an arbitrary length array.
   1. The program will look in M[0] for the number (n) of elements in the array. It will then sum the values of M[1]-M[n] and put the result in memery location M[n+1].
   2. Test for an array with zero entries, 1 entry, 5 entries and 10 entries.
   3. Turn in your program.
   4. What was the most challenging part of this program?
4. Write a program to divide two numbers and produce a quotient and a remainder.
   1. Compute M[0]/M[1] and put the quotient in M[2] and the remainder in M[3].
   2. If M[1] is zero (0), put a -1 in M[2] and M[3] and halt.
   3. Try for 4/40, 5/9, 30/7, 6/0 and 0/7.
   4. Turn in your program.
   5. What was the most challenging part of this program?
5. What did you think of this assignment? What did you learn? How much time did it take?