Greedy is an algorithmic paradigm that builds up a solution piece by piece, always choosing the next piece that offers the most obvious and immediate benefit. So the problems where choosing locally optimal also leads to global solution are the best fit for Greedy.
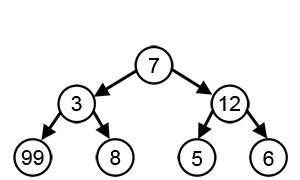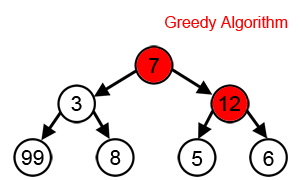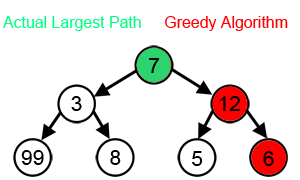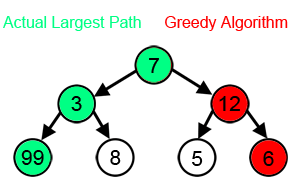
However, in many problems, a greedy strategy does not produce an optimal solution. For example, in the animation below, the greedy algorithm seeks to find the path with the largest sum. It does this by selecting the largest available number at each step. The greedy algorithm fails to find the largest sum, however, because it makes decisions based only on the information it has at any one step, without regard to the overall problem.
If both of the properties below are true, a greedy algorithm can be used to solve the problem.
- Greedy choice property: A global (overall) optimal solution can be reached by choosing the optimal choice at each step.
- Optimal substructure: A problem has an optimal substructure if an optimal solution to the entire problem contains the optimal solutions to the sub-problems.
In other words, greedy algorithms work on problems for which it is true that, at every step, there is a choice that is optimal for the problem up to that step, and after the last step, the algorithm produces the optimal solution of the complete problem.
Knapsack problem
Given a set of different items, each one with an associated value and weight, determine which items you should pick in order to maximize the value of the items without surpassing the capacity of your knapsack.
Example:
Here, we will look at one form of the knapsack problem. The knapsack problem involves deciding which subset of items you should take from a set of items if you want to optimize some value: perhaps the worth of the items, the size of the items, or the ratio of worth to size.
In this problem, we will assume that we can either take an item or leave it (we cannot take a fractional part of an item). We will also assume that there is only one of each item. Our knapsack has a fixed size, and we want to optimize the worth of the items we take, so we must choose the items we take with care.[3]
Our knapsack can hold at most 25 units of space.
Here is the list of items and their worths.
| Item | Size | Price |
| Laptop | 22 | 12 |
| PlayStation | 10 | 9 |
| Textbook | 9 | 9 |
| Basketball | 7 | 6 |
Which items do we choose to optimize for price?
There are two greedy algorithms we could propose to solve this. One has a rule that selects the item with the largest price at each step, and the other has a rule that selects the smallest sized item at each step.
- Largest-price Algorithm: At the first step, we take the laptop. We gain 12 units of worth, but can now only carry 25−22=3 units of additional space in the knapsack. Since no items that remain will fit into the bag, we can only take the laptop and have a total of 12 units of worth.
- Smallest-sized-item Algorithm: At the first step, we will take the smallest-sized item: the basketball. This gives us 66 units of worth, and leaves us with 25−7=18 units of space in our bag. Next, we select the next smallest item, the textbook. This gives us a total of 6+9=15 units of worth, and leaves us with 18−9=9 units of space. Since no remaining items are 99 units of space or less, we can take no more items.
The greedy algorithms yield solutions that give us 12 units of worth and 15 units of worth. But neither of these are the optimal solution. Inspect the table yourself and see if you can determine a better selection of items.
Taking the textbook and the PlayStation yields 9+9=18 units of worth and takes up 10+9=19 units of space. This is the optimal answer, and we can see that a greedy algorithm will not solve the knapsack problem since the greedy choice and optimal substructure properties do not hold.
Fractional Knapsack Problem
For this version, we don’t have to take all of something, we can cut it off and take part (A fraction).
For example, if you have a knapsack that can hold 50kg, and you have to choose from the following:
| Items | Platinum | Gold | Silver | Copper | Lead |
|---|---|---|---|---|---|
| Weights available (in kg) | 3 | 3 | 20 | 30 | 50 |
| Value/kg | 100 | 70 | 30 | 10 | 2 |
| Profit Value/weight | 100/3 = 33.33 | 70/3 = 23.33 | 30/20 = 1.5 | 10/30=0.333 | 2/50=0.04 |
Now we assume we can “cut off” the amount we want.
- Consider all the items with their weights and profits mentioned respectively.
- Calculate profit for each item as Vi/Wi of all the items and sort the items in descending order based on their Pi/Wi values.
- Without exceeding the limit, add the items into the knapsack.
- If the knapsack can still store some weight, but the weights of other items exceed the limit, the fractional part of the next time can be added.
- Hence, giving it the name fractional knapsack problem.
Add: All Platimum , All Gold, All Silver. That’s 3 + 3 + 20 = 23. Profit so far is 33.33+23.33+1.5 = 58.16
Then add: 24kg of copper. That’s 10/24 = 0.42 profit
Total weight is now 50kg. Profit is 58.16+0.42 = 58.58
This works!
Code
#include <iostream>
int n = 5;
int p[10] = {3, 3, 2, 5, 1};
int w[10] = {10, 15, 10, 12, 8};
int W = 10;
int main(){
int cur_w;
float tot_v;
int i, maxi;
int used[10];
for (i = 0; i < n; ++i)
used[i] = 0;
cur_w = W;
while (cur_w > 0) {
maxi = -1;
for (i = 0; i < n; ++i)
if ((used[i] == 0) &&
((maxi == -1) || ((float)w[i]/p[i] > (float)w[maxi]/p[maxi])))
maxi = i;
used[maxi] = 1;
cur_w -= p[maxi];
tot_v += w[maxi];
if (cur_w >= 0)
printf("Added object %d (%d, %d) completely in the bag. Space left: %d.\n", maxi + 1, w[maxi], p[maxi], cur_w);
else {
printf("Added %d%% (%d, %d) of object %d in the bag.\n", (int)((1 + (float)cur_w/p[maxi]) * 100), w[maxi], p[maxi], maxi + 1);
tot_v -= w[maxi];
tot_v += (1 + (float)cur_w/p[maxi]) * w[maxi];
}
}
printf("Filled the bag with objects worth %.2f.\n", tot_v);
return 0;
}