Breadth First Search for a Graph

The breadth-first search (BFS) algorithm is used to search a tree or graph data structure for a node that meets a set of criteria. It starts at the tree’s root or graph and searches/visits all nodes at the current depth level before moving on to the nodes at the next depth level. Breadth-first search can be used to solve many problems in graph theory.

Breadth-First Traversal (or Search) for a graph is similar to the Breadth-First Traversal of a tree. 

The only catch here is, that, unlike trees, graphs may contain cycles, so we may come to the same node again. To avoid processing a node more than once, we divide the vertices into two categories:

• Visited and
• Not visited.

A boolean visited array is used to mark the visited vertices. For simplicity, it is assumed that all vertices are reachable from the starting vertex. BFS uses a queue data structure for traversal.

Example: 

In the following graph, we start traversal from vertex 2.

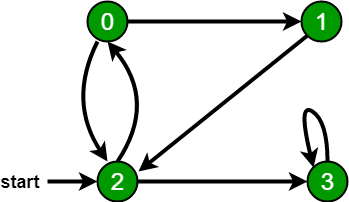
When we come to vertex 0, we look for all adjacent vertices of it. 

• 2 is also an adjacent vertex of 0. 
• If we don’t mark visited vertices, then 2 will be processed again and it will become a non-terminating process.

There can be multiple BFS traversals for a graph. Different BFS traversals for the above graph :
2, 3, 0, 1
2, 0, 3, 1

Implementation of BFS traversal on Graph:

Pseudocode:

Breadth_First_Search( Graph, X ) // Here, Graph is the graph that we already have and X is the source node

Let Q be the queue
Q.enqueue( X ) // Inserting source node X into the queue
Mark X node as visited.

While ( Q is not empty )
Y = Q.dequeue( ) // Removing the front node from the queue

Process all the neighbors of Y, For all the neighbors Z of Y
If Z is not visited, Q. enqueue( Z ) // Stores Z in Q
Mark Z as visited

Follow the below method to implement BFS traversal.

• Declare a queue and insert the starting vertex.
• Initialize a visited array and mark the starting vertex as visited.
• Follow the below process till the queue becomes empty:
  • Remove the first vertex of the queue.
  • Mark that vertex as visited.
  • Insert all the unvisited neighbors of the vertex into the queue.

Illustration:

Step1: Initially queue and visited arrays are empty.

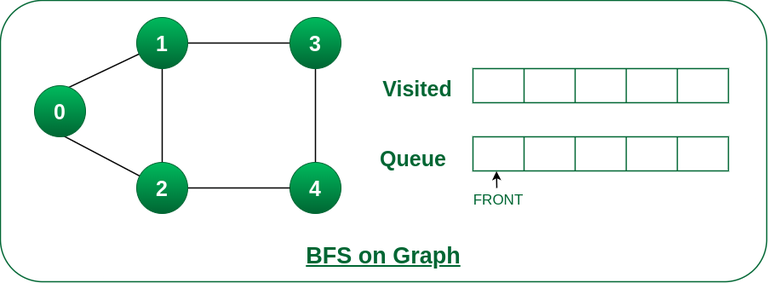
Queue and visited arrays are empty initially.

Step2: Push node 0 into queue and mark it visited.

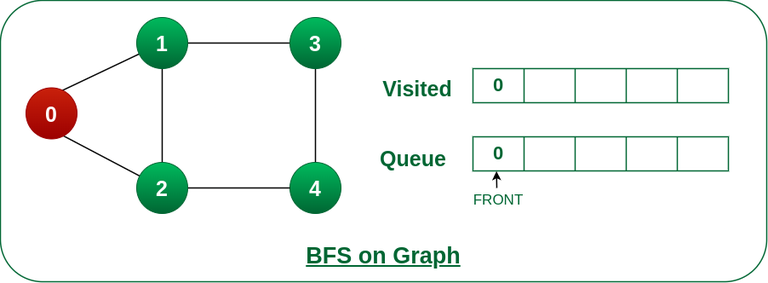
Push node 0 into queue and mark it visited.

Step 3: Remove node 0 from the front of queue and visit the unvisited neighbours and push them into queue.

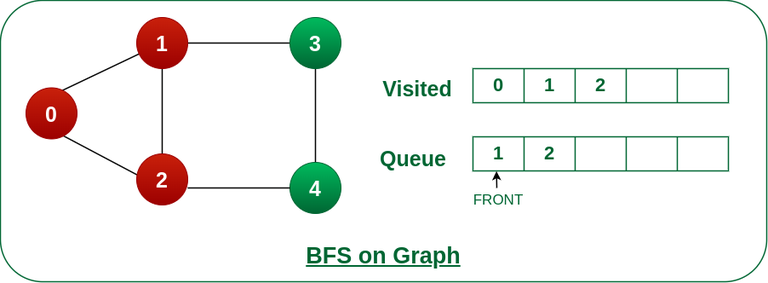
Remove node 0 from the front of queue and visited the unvisited neighbours and push into queue.

Step 4: Remove node 1 from the front of queue and visit the unvisited neighbours and push them into queue.

Remove node 1 from the front of queue and visited the unvisited neighbours and push

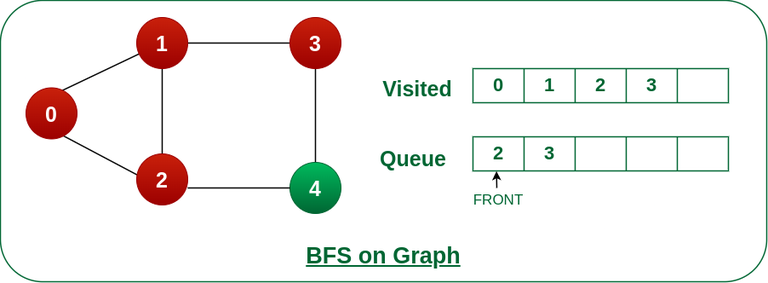
Step 5: Remove node 2 from the front of queue and visit the unvisited neighbours and push them into queue.

Remove node 2 from the front of queue and visit the unvisited neighbours and push them into queue.

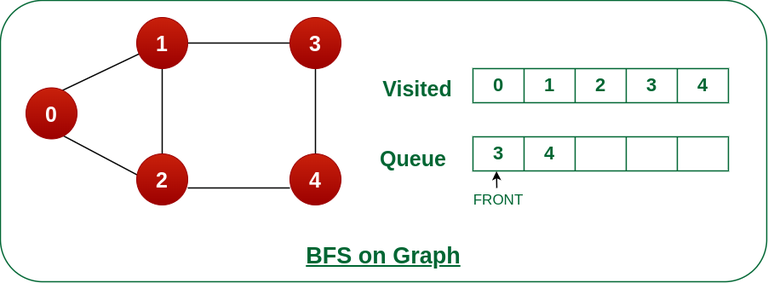
Step 6: Remove node 3 from the front of queue and visit the unvisited neighbours and push them into queue. 
As we can see that every neighbours of node 3 is visited, so move to the next node that are in the front of the queue.

Remove node 3 from the front of queue and visit the unvisited neighbours and push them into queue. 

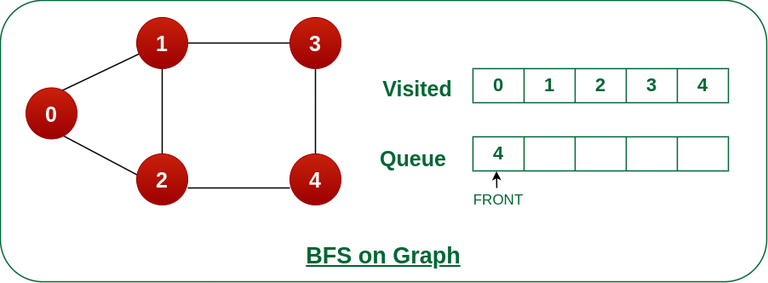
Steps 7: Remove node 4 from the front of queue and visit the unvisited neighbours and push them into queue. 
As we can see that every neighbours of node 4 are visited, so move to the next node that is in the front of the queue.

Remove node 4 from the front of queue and visit the unvisited neighbours and push them into queue.

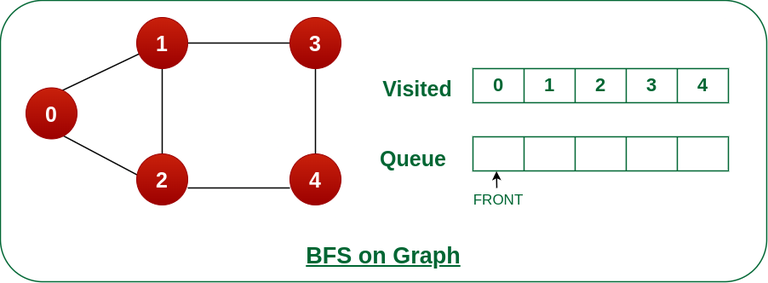
Now, Queue becomes empty, So, terminate these process of iteration.

The implementation uses an adjacency list representation of graphs. STL‘s list container stores lists of adjacent nodes and the queue of nodes needed for BFS traversal.

Code (Github code)

#include <iostream>
#include <vector>
#include <list>
#include <queue>

using namespace std;

// This class represents a directed graph using an adjacency list representation
class Graph {
    int V;                     // Number of vertices
    vector<list<int>> adj;     // Adjacency lists for each vertex

public:
    // Constructor
    Graph(int V);

    // Function to add an edge to the graph
    void addEdge(int v, int w);

    // Function to print BFS traversal from a given source vertex
    void BFS(int s);
};

// Initialize graph with a given number of vertices
Graph::Graph(int V) : V(V), adj(V) {}

// Add an edge to the graph (directed)
void Graph::addEdge(int v, int w) {
    adj[v].push_back(w);  // Add w to v’s adjacency list
}

// Perform BFS traversal from a given source vertex
void Graph::BFS(int s) {
    // Vector to track visited vertices
    vector<bool> visited(V, false);

    // Queue for BFS
    queue<int> q;

    // Mark the source vertex as visited and enqueue it
    visited[s] = true;
    q.push(s);

    while (!q.empty()) {
        // Dequeue a vertex from the queue and print it
        int vertex = q.front();
        cout << vertex << " ";
        q.pop();

        // Get all adjacent vertices of the dequeued vertex
        // If an adjacent vertex has not been visited, mark it as visited and enqueue it
        for (int adjVertex : adj[vertex]) {
            if (!visited[adjVertex]) {
                visited[adjVertex] = true;
                q.push(adjVertex);
            }
        }
    }
}

// Driver program to test methods of the Graph class
int main() {
    // Create a graph
    Graph g(4);
    g.addEdge(0, 1);
    g.addEdge(0, 2);
    g.addEdge(1, 2);
    g.addEdge(2, 0);
    g.addEdge(2, 3);
    g.addEdge(3, 3);

    cout << "Following is Breadth-First Traversal (starting from vertex 2):\n";
    g.BFS(2);

    return 0;
}