Binary Tree Traversal

Github Code

Unlike linear data structures (Array, Linked List, Queues, Stacks, etc) which have only one logical way to traverse them, trees can be traversed in different ways. The following are the generally used methods for traversing trees:

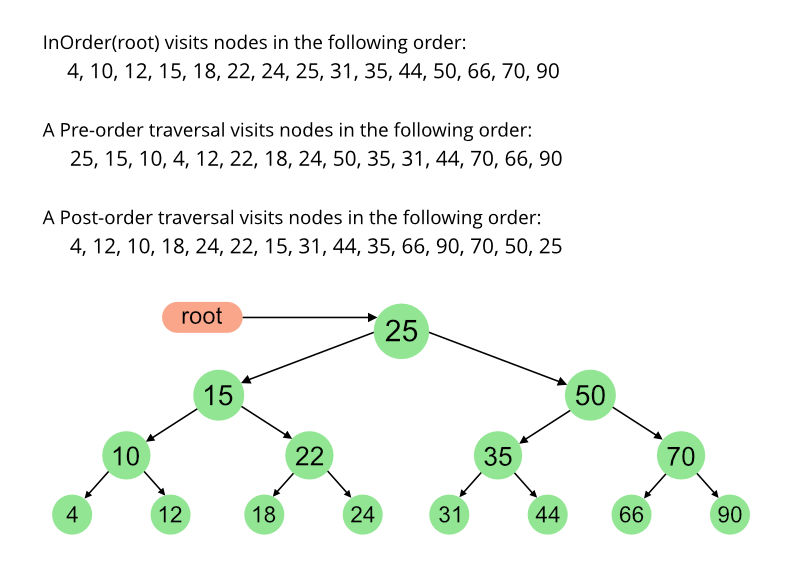
Inorder Traversal

Algorithm Inorder(tree)

1. Traverse the left subtree, i.e., call Inorder(left->subtree)
2. Visit the root.
3. Traverse the right subtree, i.e., call Inorder(right->subtree)

Uses of Inorder Traversal:

In the case of binary search trees (BST), Inorder traversal gives nodes in non-decreasing order. To get nodes of BST in non-increasing order, a variation of Inorder traversal where Inorder traversal is reversed can be used. 
Repl code for inorder traversal

Code

// In-order traversal: Left, Root, Right
void inorderTraversal(Node* root) {
    if (root != nullptr) {
        inorderTraversal(root->left);
        cout << root->key << " ";
        inorderTraversal(root->right);
    }
}

Preorder Tree Traversal

Algorithm Preorder(tree)

1. Visit the root.
2. Traverse the left subtree, i.e., call Preorder(left->subtree)
3. Traverse the right subtree, i.e., call Preorder(right->subtree) 

Code

// Pre-order traversal: Root, Left, Right
void preorderTraversal(Node* root) {
    if (root != nullptr) {
        cout << root->key << " ";
        preorderTraversal(root->left);
        preorderTraversal(root->right);
    }
}

Postorder Traversal

Algorithm Postorder(tree)

1. Traverse the left subtree, i.e., call Postorder(left->subtree)
2. Traverse the right subtree, i.e., call Postorder(right->subtree)
3. Visit the root

Code

// Post-order traversal: Left, Right, Root
void postorderTraversal(Node* root) {
    if (root != nullptr) {
        postorderTraversal(root->left);
        postorderTraversal(root->right);
        cout << root->key << " ";
    }
}