A binary Search Tree is a node-based binary tree data structure which has the following properties:
- The left subtree of a node contains only nodes with keys lesser than the node’s key.
- The right subtree of a node contains only nodes with keys greater than the node’s key.
- The left and right subtree each must also be a binary search tree.
There must be no duplicate nodes.

The above properties of the Binary Search Tree provide an ordering among keys so that the operations like search, minimum and maximum can be done fast. If there is no order, then we may have to compare every key to search for a given key.
Basic operations on a BST
- Create: creates an empty tree.
- Insert: insert a node in the tree.
- Search: Searches for a node in the tree.
- Delete: deletes a node from the tree.
- Inorder: in-order traversal of the tree.
- Preorder: pre-order traversal of the tree.
- Postorder: post-order traversal of the tree.
Tree Definition
// Method 2: Using "class" to make
// user-define data type
class Node {
public:
int data;
Node* left;
Node* right;
};
Search BST
Recursive! You want to search for key. Start at root node. there are four cases:
- node = null. Fail, not found.
- The node.data == key. Success, found it!
- The node.data > key. Search left sub tree.
- The node.data < key. Search left sub tree.
In the tree above, try to find 4, 10, 3, and 20.
// C function to search a given key in a given BST
struct node* search(struct node* root, int key)
{
// Base Cases: root is null or key is present at root
if (root == NULL || root->key == key)
return root;
// Key is greater than root's key
if (root->key < key)
return search(root->right, key);
// Key is smaller than root's key
return search(root->left, key);
}
Time complexity: O(h), where h is the height of the BST.
Space complexity: O(h), where h is the height of the BST. This is because the maximum amount of space needed to store the recursion stack would be h.
Insert a new node
A new key is always inserted at the leaf. We start searching for a key from the root until we hit a leaf node. Once a leaf node is found, the new node is added as a child of the leaf node.
100 100
/ \ Insert 40 / \
20 500 ———> 20 500
/ \ / \
10 30 10 30
\
40Consider starting with an empty tree and adding:
10 5 15 2 7 12 20 6 9 18 14
Now try
1 3 5 6 9 12 14 18 20 23 25
What’s the problem here?
Insert Implementation
// C++ program to demonstrate insertion
// in a BST recursively.
#include <iostream>
using namespace std;
class BST {
int data;
BST *left, *right;
public:
// Default constructor.
BST();
// Parameterized constructor.
BST(int);
// Insert function.
BST* Insert(BST*, int);
// Inorder traversal.
void Inorder(BST*);
};
// Default Constructor definition.
BST ::BST()
: data(0)
, left(NULL)
, right(NULL)
{
}
// Parameterized Constructor definition.
BST ::BST(int value)
{
data = value;
left = right = NULL;
}
// Insert function definition.
BST* BST ::Insert(BST* root, int value)
{
if (!root) {
// Insert the first node, if root is NULL.
return new BST(value);
}
// Insert data.
if (value > root->data) {
// Insert right node data, if the 'value'
// to be inserted is greater than 'root' node data.
// Process right nodes.
root->right = Insert(root->right, value);
}
else if (value < root->data){
// Insert left node data, if the 'value'
// to be inserted is smaller than 'root' node data.
// Process left nodes.
root->left = Insert(root->left, value);
}
// Return 'root' node, after insertion.
return root;
}
// Inorder traversal function.
// This gives data in sorted order.
void BST ::Inorder(BST* root)
{
if (!root) {
return;
}
Inorder(root->left);
cout << root->data << endl;
Inorder(root->right);
}
// Driver code
int main()
{
BST b, *root = NULL;
root = b.Insert(root, 50);
b.Insert(root, 30);
b.Insert(root, 20);
b.Insert(root, 40);
b.Insert(root, 70);
b.Insert(root, 60);
b.Insert(root, 80);
b.Inorder(root);
return 0;
}Time Complexity: The worst-case time complexity of search and insert operations is O(h) where h is the height of the Binary Search Tree. In the worst case, we may have to travel from the root to the deepest leaf node. The height of a skewed tree may become n and the time complexity of the search and insert operation may become O(n).
Auxiliary Space: O(1)
BST Delete
How to delete? Three cases:
1) Node to be deleted is the leaf: Simply remove it from the tree.
<code><code data-enlighter-language="generic" class="EnlighterJSRAW"> 50 50
/ \ delete(20) / \
30 70 ———> 30 70
/ \ / \ \ / \
20 40 60 80 40 60 80</code></code>Code language: HTML, XML (xml)2) Node to be deleted has only one child: Copy the child to the node and delete the node.
50 50
/ \ delete(30) / \
30 70 ———> 40 70
\ / \ / \
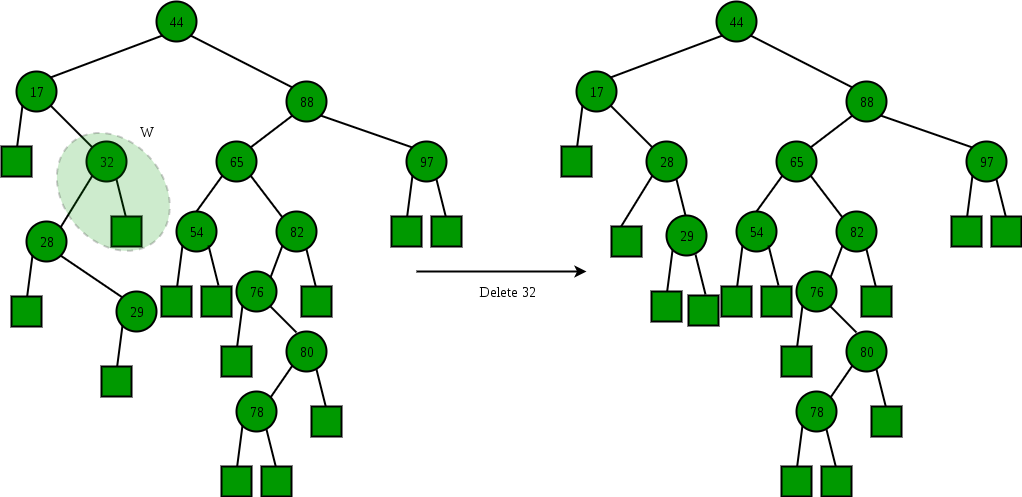
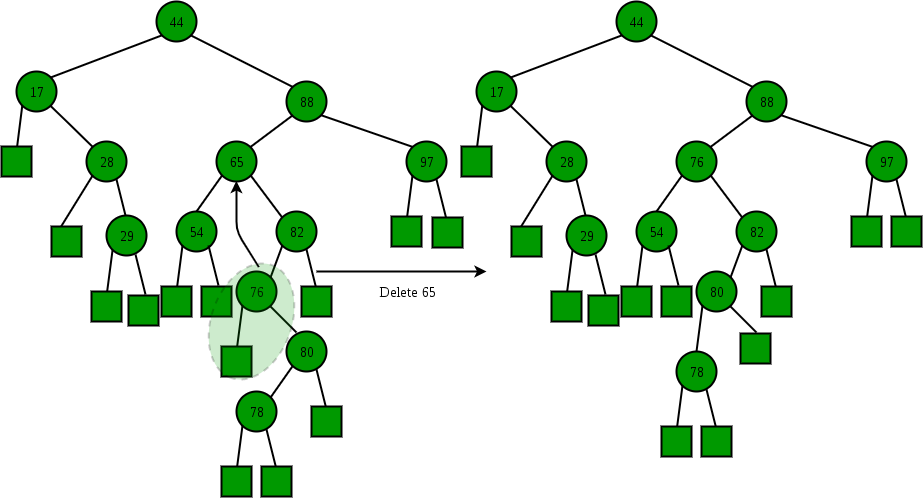
40 60 80 60 80Code language: JavaScript (javascript)3) Node to be deleted has two children: Find inorder successor of the node. Copy contents of the inorder successor to the node and delete the inorder successor.
Note: Inorder predecessor can also be used.
50 60
/ \ delete(50) / \
40 70 ———> 40 70
/ \ \
60 80 80Code language: JavaScript (javascript)Note: Inorder successor is needed only when the right child is not empty. In this particular case, in-order successor can be obtained by finding the minimum value in the right child of the node.
Follow the below steps to solve the problem:
- If the root is NULL, then return root (Base case)
- If the key is less than the root’s value, then set root->left = deleteNode(root->left, key)
- If the key is greater than the root’s value, then set root->right = deleteNode(root->right, key)
- Else check
- If the root is a leaf node then return null
- else if it has only the left child, then return the left child
- else if it has only the right child, then return the right child
- else set the value of root as of its inorder successor and recur to delete the node with the value of the inorder successor
- Return
Complete Code (github)
#include <iostream>
// Node class representing a node in the binary search tree
class Node {
public:
int key;
Node* left;
Node* right;
// Constructor to initialize the node
Node(int item) : key(item), left(nullptr), right(nullptr) {}
};
// Utility function to perform an inorder traversal of the BST
void inorderTraversal(Node* root) {
if (root != nullptr) {
inorderTraversal(root->left);
std::cout << root->key << " ";
inorderTraversal(root->right);
}
}
// Utility function to insert a new node with a given key into the BST
Node* insertNode(Node* root, int key) {
if (root == nullptr)
return new Node(key);
if (key < root->key)
root->left = insertNode(root->left, key);
else
root->right = insertNode(root->right, key);
return root;
}
// Utility function to find the node with the minimum key value in the BST
Node* minValueNode(Node* node) {
Node* current = node;
while (current && current->left != nullptr)
current = current->left;
return current;
}
// Function to delete a node with a given key and return the new root
Node* deleteNode(Node* root, int key) {
if (root == nullptr)
return root;
if (key < root->key)
root->left = deleteNode(root->left, key);
else if (key > root->key)
root->right = deleteNode(root->right, key);
else {
// Node to be deleted found
if (root->left == nullptr) {
Node* temp = root->right;
delete root;
return temp;
} else if (root->right == nullptr) {
Node* temp = root->left;
delete root;
return temp;
}
// Node with two children: find the inorder successor (smallest in the right subtree)
Node* temp = minValueNode(root->right);
root->key = temp->key; // Copy the inorder successor's key to this node
root->right = deleteNode(root->right, temp->key); // Delete the inorder successor
}
return root;
}
// Main function to demonstrate BST insertion, deletion, and traversal
int main() {
Node* root = nullptr;
root = insertNode(root, 50);
insertNode(root, 30);
insertNode(root, 20);
insertNode(root, 40);
insertNode(root, 70);
insertNode(root, 60);
insertNode(root, 80);
std::cout << "Inorder traversal of the given tree: ";
inorderTraversal(root);
std::cout << std::endl;
// Perform deletions
std::cout << "\nDeleting 20\n";
root = deleteNode(root, 20);
std::cout << "Inorder traversal after deletion: ";
inorderTraversal(root);
std::cout << std::endl;
std::cout << "\nDeleting 30\n";
root = deleteNode(root, 30);
std::cout << "Inorder traversal after deletion: ";
inorderTraversal(root);
std::cout << std::endl;
std::cout << "\nDeleting 50\n";
root = deleteNode(root, 50);
std::cout << "Inorder traversal after deletion: ";
inorderTraversal(root);
std::cout << std::endl;
return 0;
}
Time Complexity: O(log N)
Auxiliary Space: O(log N), Space used for recursion stack
