AVL tree is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.
Example of AVL Tree:
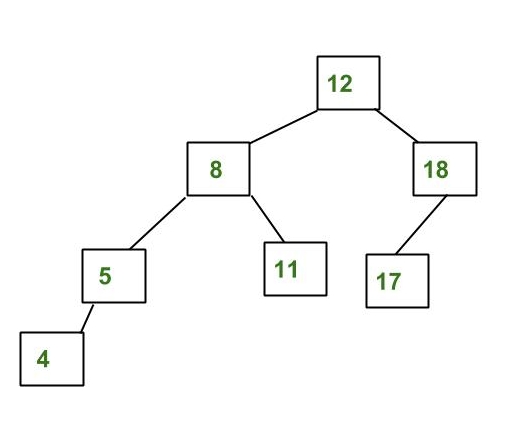
The above tree is AVL because the differences between the heights of left and right subtrees for every node are less than or equal to 1.
Example of a Tree that is NOT an AVL Tree:
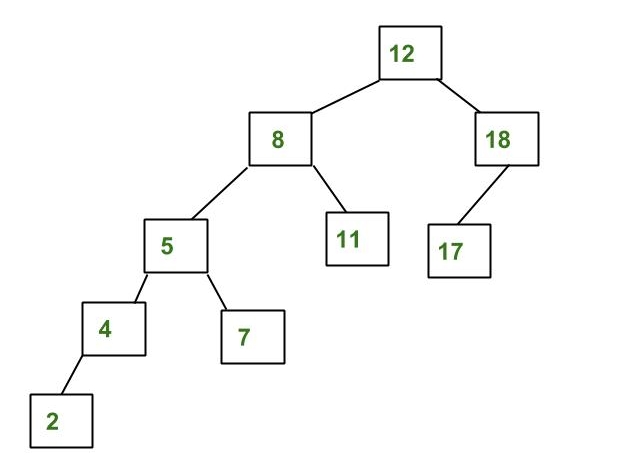
The above tree is not AVL because the differences between the heights of the left and right subtrees for 8 and 12 are greater than 1.
Why AVL Trees?
Most of the BST operations (e.g., search, max, min, insert, delete.. etc) take O(h) time where h is the height of the BST. The cost of these operations may become O(n) for a skewed Binary tree. If we make sure that the height of the tree remains O(log(n)) after every insertion and deletion, then we can guarantee an upper bound of O(log(n)) for all these operations. The height of an AVL tree is always O(log(n)) where n is the number of nodes in the tree.
Insertion in AVL Tree:
To make sure that the given tree remains AVL after every insertion, we must augment the standard BST insert operation to perform some re-balancing.
Following are two basic operations that can be performed to balance a BST without violating the BST property (keys(left) < key(root) < keys(right)).
- Left Rotation
- Right Rotation
T1, T2 and T3 are subtrees of the tree, rooted with y (on the left side) or x (on the right side)
y x
/ \ Right Rotation / \
x T3 - - - - - - - > T1 y
/ \ < - - - - - - - / \
T1 T2 Left Rotation T2 T3
Keys in both of the above trees follow the following order
keys(T1) < key(x) < keys(T2) < key(y) < keys(T3)
So BST property is not violated anywhere.
Steps to follow for insertion:
Let the newly inserted node be w
- Perform standard BST insert for w.
- Starting from w, travel up and find the first unbalanced node. Let z be the first unbalanced node, y be the child of z that comes on the path from w to z and x be the grandchild of z that comes on the path from w to z.
- Re-balance the tree by performing appropriate rotations on the subtree rooted with z. There can be 4 possible cases that need to be handled as x, y and z can be arranged in 4 ways.
- Following are the possible 4 arrangements:
- y is the left child of z and x is the left child of y (Left Left Case)
- y is the left child of z and x is the right child of y (Left Right Case)
- y is the right child of z and x is the right child of y (Right Right Case)
- y is the right child of z and x is the left child of y (Right Left Case)
Following are the operations to be performed in above mentioned 4 cases. In all of the cases, we only need to re-balance the subtree rooted with z and the complete tree becomes balanced as the height of the subtree (After appropriate rotations) rooted with z becomes the same as it was before insertion.
1. Left Left Case
T1, T2, T3 and T4 are subtrees.
z y
/ \ / \
y T4 Right Rotate (z) x z
/ \ - - - - - - - - -> / \ / \
x T3 T1 T2 T3 T4
/ \
T1 T2
2. Left Right Case
z z x
/ \ / \ / \
y T4 Left Rotate (y) x T4 Right Rotate(z) y z
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
T1 x y T3 T1 T2 T3 T4
/ \ / \
T2 T3 T1 T2
3. Right Right Case
z y
/ \ / \
T1 y Left Rotate(z) z x
/ \ - - - - - - - -> / \ / \
T2 x T1 T2 T3 T4
/ \
T3 T4
4. Right Left Case
z z x
/ \ / \ / \
T1 y Right Rotate (y) T1 x Left Rotate(z) z y
/ \ - - - - - - - - -> / \ - - - - - - - -> / \ / \
x T4 T2 y T1 T2 T3 T4
/ \ / \
T2 T3 T3 T4
Illustration of Insertion at AVL Tree
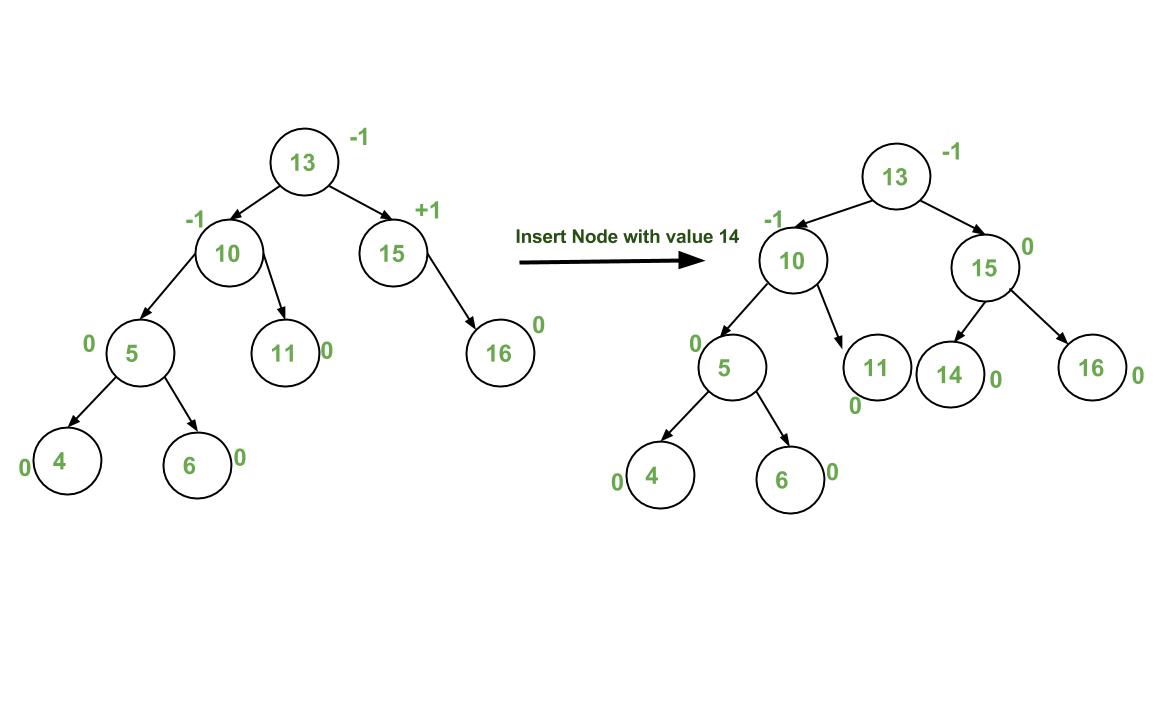
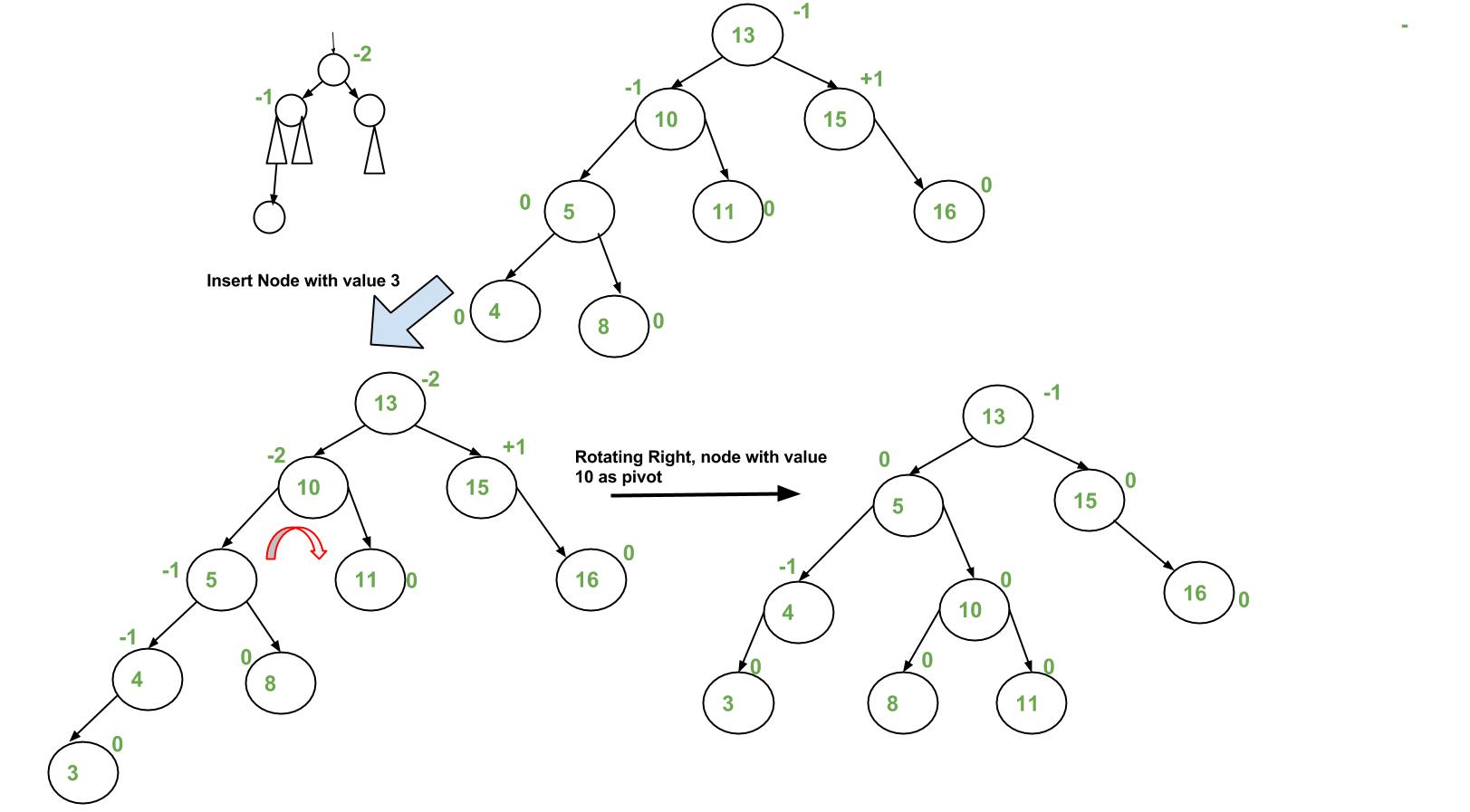
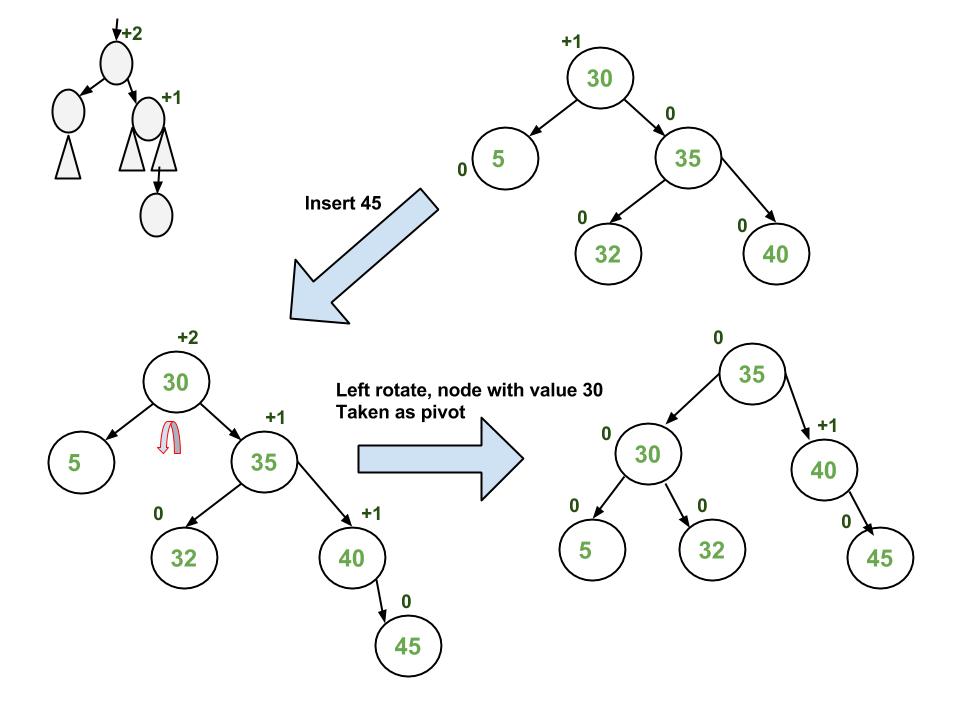
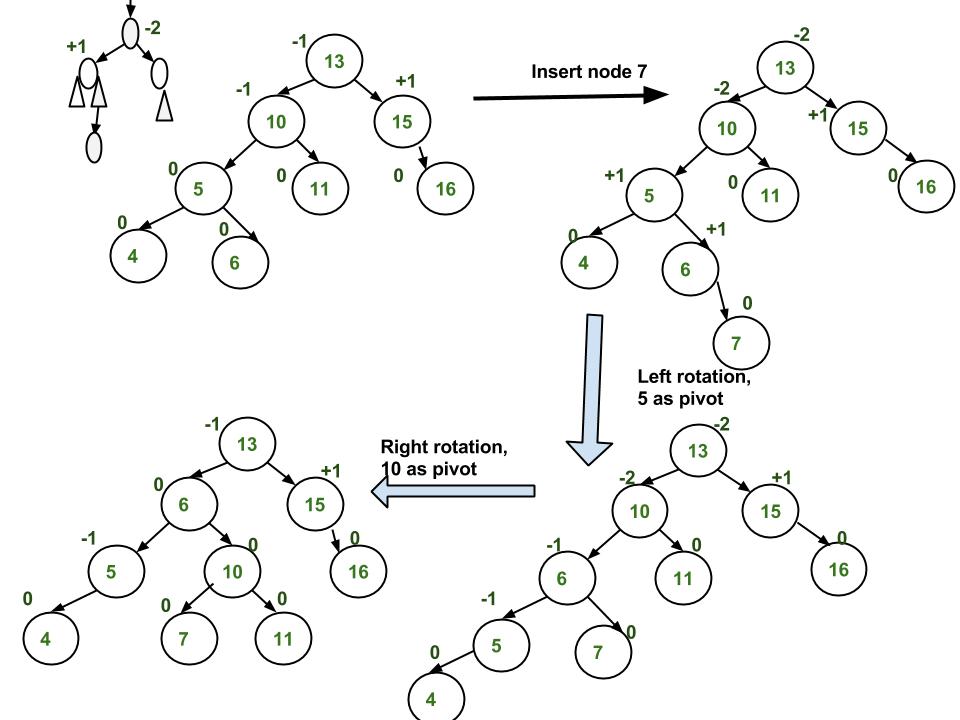

Approach:
The idea is to use recursive BST insert, after insertion, we get pointers to all ancestors one by one in a bottom-up manner. So we don’t need a parent pointer to travel up. The recursive code itself travels up and visits all the ancestors of the newly inserted node.
Follow the steps mentioned below to implement the idea:
- Perform the normal BST insertion.
- The current node must be one of the ancestors of the newly inserted node. Update the height of the current node.
- Get the balance factor (left subtree height – right subtree height) of the current node.
- If the balance factor is greater than 1, then the current node is unbalanced and we are either in the Left Left case or left Right case. To check whether it is left left case or not, compare the newly inserted key with the key in the left subtree root.
- If the balance factor is less than -1, then the current node is unbalanced and we are either in the Right Right case or Right-Left case. To check whether it is the Right Right case or not, compare the newly inserted key with the key in the right subtree root.
Code (github):
#include <iostream>
#include <algorithm> // For std::max
// AVL tree node structure
class Node {
public:
int key;
Node* left;
Node* right;
int height;
// Constructor to initialize a node
Node(int value) : key(value), left(nullptr), right(nullptr), height(1) {}
};
// Function to get the height of a node
int getHeight(Node* node) {
return node ? node->height : 0;
}
// Function to get the balance factor of a node
int getBalance(Node* node) {
return node ? getHeight(node->left) - getHeight(node->right) : 0;
}
// Right rotation function
Node* rightRotate(Node* y) {
Node* x = y->left;
Node* T2 = x->right;
// Perform rotation
x->right = y;
y->left = T2;
// Update heights
y->height = std::max(getHeight(y->left), getHeight(y->right)) + 1;
x->height = std::max(getHeight(x->left), getHeight(x->right)) + 1;
return x; // Return new root
}
// Left rotation function
Node* leftRotate(Node* x) {
Node* y = x->right;
Node* T2 = y->left;
// Perform rotation
y->left = x;
x->right = T2;
// Update heights
x->height = std::max(getHeight(x->left), getHeight(x->right)) + 1;
y->height = std::max(getHeight(y->left), getHeight(y->right)) + 1;
return y; // Return new root
}
// Insert a key into the AVL tree and balance the tree
Node* insert(Node* node, int key) {
if (node == nullptr) {
return new Node(key); // Create a new node if tree/subtree is empty
}
// Perform normal BST insertion
if (key < node->key) {
node->left = insert(node->left, key);
} else if (key > node->key) {
node->right = insert(node->right, key);
} else {
return node; // Duplicate keys are not allowed
}
// Update height of the node
node->height = 1 + std::max(getHeight(node->left), getHeight(node->right));
// Check the balance factor of the node to see if it became unbalanced
int balance = getBalance(node);
// Left Left Case
if (balance > 1 && key < node->left->key) {
return rightRotate(node);
}
// Right Right Case
if (balance < -1 && key > node->right->key) {
return leftRotate(node);
}
// Left Right Case
if (balance > 1 && key > node->left->key) {
node->left = leftRotate(node->left);
return rightRotate(node);
}
// Right Left Case
if (balance < -1 && key < node->right->key) {
node->right = rightRotate(node->right);
return leftRotate(node);
}
return node; // Return the unchanged node pointer
}
// Pre-order traversal function to print keys of the AVL tree
void preOrder(Node* root) {
if (root != nullptr) {
std::cout << root->key << " ";
preOrder(root->left);
preOrder(root->right);
}
}
// Function to delete the entire tree and free memory
void deleteTree(Node* node) {
if (node != nullptr) {
deleteTree(node->left);
deleteTree(node->right);
delete node;
}
}
// Main function to demonstrate AVL tree insertion and traversal
int main() {
Node* root = nullptr;
// Insert nodes into the AVL tree
root = insert(root, 10);
root = insert(root, 20);
root = insert(root, 30);
root = insert(root, 40);
root = insert(root, 50);
root = insert(root, 25);
/* The constructed AVL Tree will look like this:
30
/ \
20 40
/ \ \
10 25 50
*/
std::cout << "Pre-order traversal of the constructed AVL tree: ";
preOrder(root);
std::cout << std::endl;
// Clean up the tree and free memory
deleteTree(root);
return 0;
}
Complexity Analysis
| Operation | Average-Case | Worst-Case |
|---|---|---|
| Traversal | O (n) | O(n) |
| Searching | O (log n) | O(log n) |
| Insertion | O (log n) | O(log n) |
| Deletion | O (log n) | O(log n) |
