Huffman Coding Example

Here’s a complete example of constructing a Huffman Tree for a code with 6 characters. We’ll walk through the process step-by-step, including the tree construction and the final codes for each character.

Input Characters and Frequencies

Character	Frequency
A	5
B	9
C	12
D	13
E	16
F	45

Step 1: Initialize Priority Queue

Each character is treated as a leaf node in the tree. We’ll use a priority queue (min-heap) to store the nodes, sorted by frequency.

Initial Priority Queue:
[A:5, B:9, C:12, D:13, E:16, F:45]

Step 2: Build the Huffman Tree

Iteration 1: Combine Two Smallest Nodes

Remove A:5 and B:9 (smallest frequencies).
Create a new node with frequency = 5 + 9 = 14 and children A and B.

Updated Priority Queue:

[C:12, D:13, E:16, F:45, (AB):14]

Iteration 2: Combine Two Smallest Nodes

Remove C:12 and D:13.
Create a new node with frequency = 12 + 13 = 25 and children C and D.

Updated Priority Queue:

[E:16, F:45, (AB):14, (CD):25]

Iteration 3: Combine Two Smallest Nodes

Remove (AB):14 and E:16.
Create a new node with frequency = 14 + 16 = 30 and children (AB) and E.

Updated Priority Queue:

[F:45, (CD):25, (ABE):30]

Iteration 4: Combine Two Smallest Nodes

Remove (CD):25 and (ABE):30.
Create a new node with frequency = 25 + 30 = 55 and children (CD) and (ABE).

Updated Priority Queue:

[F:45, (CDEAB):55]

Iteration 5: Combine Two Smallest Nodes

Remove F:45 and (CDEAB):55.
Create a new node with frequency = 45 + 55 = 100 and children F and (CDEAB).

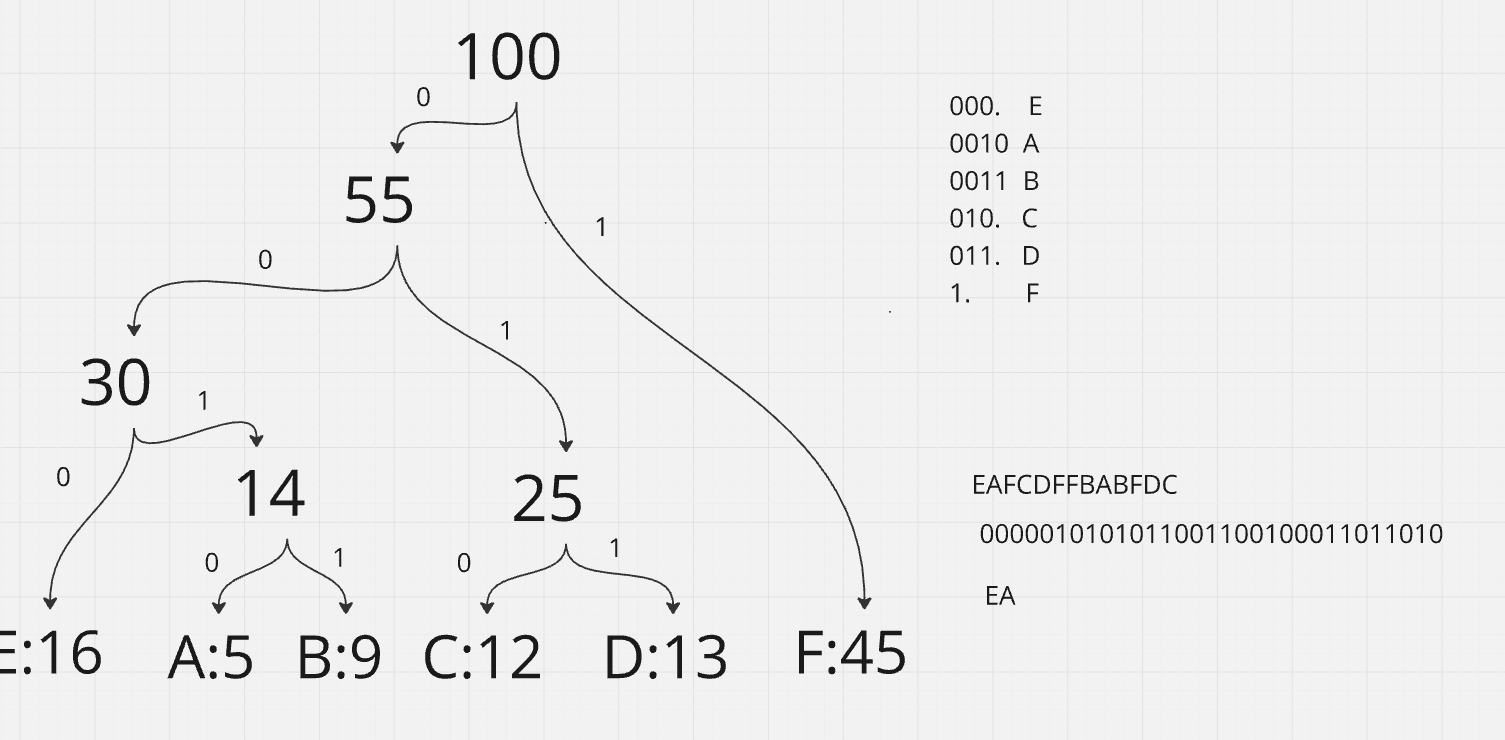
Final Huffman Tree Root:

[(F):45, (CDEAB):55] -> Root

Step 3: Assign Codes

Now traverse the Huffman Tree to assign binary codes:

Assign 0 to the left child and 1 to the right child recursively.

Tree Structure:
          (Root: 100)
         /          \
      (F: 45)     (CDEAB: 55)
                 /           \
            (CD: 25)       (ABE: 30)
           /     \         /      \
        (C:12) (D:13)  (AB:14)  (E:16)
                         /    \
                      (A:5) (B:9)

Codes:
F -> 0
C -> 100
D -> 101
A -> 1100
B -> 1101
E -> 111

Step 4: Output the Huffman Codes

Character	Code
A	1100
B	1101
C	100
D	101
E	111
F	0

Benefits of Huffman Coding

Huffman coding minimizes the total length of the encoded message by assigning shorter codes to more frequent characters and longer codes to less frequent ones. This makes it highly efficient for compression tasks.

Resulting codes:

Input Characters and Frequencies

Character	Frequency
A	5
B	9
C	12
D	13
E	16
F	45

Step 1: Initialize Priority Queue

Each character is treated as a leaf node in the tree. We’ll use a priority queue (min-heap) to store the nodes, sorted by frequency.

mathematicaCopy codeInitial Priority Queue:
[A:5, B:9, C:12, D:13, E:16, F:45]

Step 2: Build the Huffman Tree

Iteration 1: Combine Two Smallest Nodes

Remove A:5 and B:9 (smallest frequencies).
Create a new node with frequency = 5 + 9 = 14 and children A and B.

Updated Priority Queue:

mathematicaCopy code[C:12, D:13, E:16, F:45, (AB):14]

Iteration 2: Combine Two Smallest Nodes

Remove C:12 and D:13.
Create a new node with frequency = 12 + 13 = 25 and children C and D.

Updated Priority Queue:

csharpCopy code[E:16, F:45, (AB):14, (CD):25]

Iteration 3: Combine Two Smallest Nodes

Remove (AB):14 and E:16.
Create a new node with frequency = 14 + 16 = 30 and children (AB) and E.

Updated Priority Queue:

csharpCopy code[F:45, (CD):25, (ABE):30]

Iteration 4: Combine Two Smallest Nodes

Remove (CD):25 and (ABE):30.
Create a new node with frequency = 25 + 30 = 55 and children (CD) and (ABE).

Updated Priority Queue:

csharpCopy code[F:45, (CDEAB):55]

Iteration 5: Combine Two Smallest Nodes

Remove F:45 and (CDEAB):55.
Create a new node with frequency = 45 + 55 = 100 and children F and (CDEAB).

Final Huffman Tree Root:

cssCopy code[(F):45, (CDEAB):55] -> Root

Step 3: Assign Codes

Now traverse the Huffman Tree to assign binary codes:

Assign 0 to the left child and 1 to the right child recursively.

lessCopy codeTree Structure:
          (Root: 100)
         /          \
      (F: 45)     (CDEAB: 55)
                 /           \
            (CD: 25)       (ABE: 30)
           /     \         /      \
        (C:12) (D:13)  (AB:14)  (E:16)
                         /    \
                      (A:5) (B:9)

Codes:
F -> 0
C -> 100
D -> 101
A -> 1100
B -> 1101
E -> 111

Step 4: Output the Huffman Codes

Character	Code
A	1100
B	1101
C	100
D	101
E	111
F	0