Given a graph and a source vertex in the graph, find the shortest paths from the source to all vertices in the given graph.
Examples:
Input: src = 0, the graph is shown below.
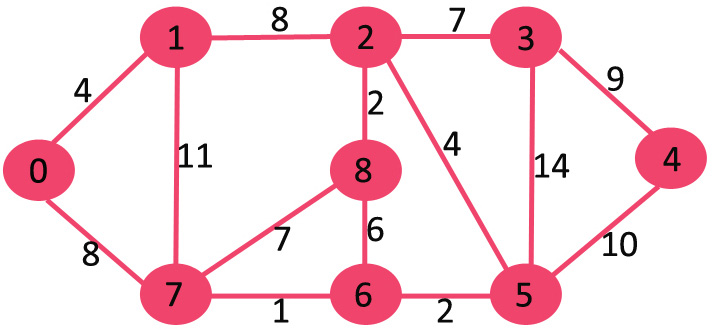
Output: 0 4 12 19 21 11 9 8 14
Explanation: The distance from 0 to 1 = 4.
The minimum distance from 0 to 2 = 12. 0->1->2
The minimum distance from 0 to 3 = 19. 0->1->2->3
The minimum distance from 0 to 4 = 21. 0->7->6->5->4
The minimum distance from 0 to 5 = 11. 0->7->6->5
The minimum distance from 0 to 6 = 9. 0->7->6
The minimum distance from 0 to 7 = 8. 0->7
The minimum distance from 0 to 8 = 14. 0->1->2->8
Follow the steps below to solve the problem:
- Create a set sptSet (shortest path tree set) that keeps track of vertices included in the shortest path tree, i.e., whose minimum distance from the source is calculated and finalized. Initially, this set is empty.
- Assign a distance value to all vertices in the input graph. Initialize all distance values as INFINITE. Assign the distance value as 0 for the source vertex so that it is picked first.
- While sptSet doesn’t include all vertices
- Pick a vertex u that is not there in sptSet and has a minimum distance value.
- Include u to sptSet.
- Then update the distance value of all adjacent vertices of u.
- To update the distance values, iterate through all adjacent vertices.
- For every adjacent vertex v, if the sum of the distance value of u (from source) and weight of edge u-v, is less than the distance value of v, then update the distance value of v.
Note: We use a boolean array sptSet[] to represent the set of vertices included in SPT. If a value sptSet[v] is true, then vertex v is included in SPT, otherwise not. Array dist[] is used to store the shortest distance values of all vertices.
Below is the illustration of the above approach:
Illustration:
To understand the Dijkstra’s Algorithm lets take a graph and find the shortest path from source to all nodes.
Consider below graph and src = 0

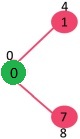
Step 1:
- The set sptSet is initially empty and distances assigned to vertices are {0, INF, INF, INF, INF, INF, INF, INF} where INF indicates infinite.
- Now pick the vertex with a minimum distance value. The vertex 0 is picked, include it in sptSet. So sptSet becomes {0}. After including 0 to sptSet, update distance values of its adjacent vertices.
- Adjacent vertices of 0 are 1 and 7. The distance values of 1 and 7 are updated as 4 and 8.
The following subgraph shows vertices and their distance values, only the vertices with finite distance values are shown. The vertices included in SPT are shown in green colour.
Step 2:
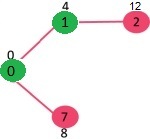
- Pick the vertex with minimum distance value and not already included in SPT (not in sptSET). The vertex 1 is picked and added to sptSet.
- So sptSet now becomes {0, 1}. Update the distance values of adjacent vertices of 1.
- The distance value of vertex 2 becomes 12.
Step 3:
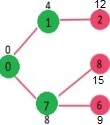
- Pick the vertex with minimum distance value and not already included in SPT (not in sptSET). Vertex 7 is picked. So sptSet now becomes {0, 1, 7}.
- Update the distance values of adjacent vertices of 7. The distance value of vertex 6 and 8 becomes finite (15 and 9 respectively).
Step 4:
- Pick the vertex with minimum distance value and not already included in SPT (not in sptSET). Vertex 6 is picked. So sptSet now becomes {0, 1, 7, 6}.
- Update the distance values of adjacent vertices of 6. The distance value of vertex 5 and 8 are updated.
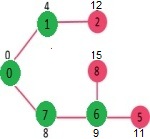
We repeat the above steps until sptSet includes all vertices of the given graph. Finally, we get the following Shortest Path Tree (SPT).

Implementation
Below is code that uses a priority queue to pick the next minimum edge.
Priority Queue Overview
In C++, a priority queue is a container that provides constant-time access to the largest (or smallest) element in the container. By default, priority_queue in C++ is a max-heap, meaning it keeps the largest element at the top. However, we can customize it to function as a min-heap by specifying a different comparator.
Breakdown of Each Component
pair<int, int>: This is the type of elements stored in the priority queue. In this case, each element is apair<int, int>, where:- The first
intrepresents a key or a distance (e.g., a distance in Dijkstra’s algorithm). - The second
inttypically represents a node or vertex associated with that key.
- The first
vector<pair<int, int>>: This is the underlying container type for the priority queue. Here,std::vectoris used as the container to store elements of typepair<int, int>.- C++ priority queues default to using a
vectoras the underlying container, but you could use other container types likedeque.
- C++ priority queues default to using a
greater<pair<int, int>>: This specifies the comparison function used by the priority queue to order elements.- By default,
priority_queueis a max-heap, meaning it will keep the largest element on top. - Specifying
greater<pair<int, int>>changes this to a min-heap, where the smallest element is kept on top. - Here, the
greatercomparator compares elements by the first element in each pair (thefirstelement ofpair<int, int>). This is useful in algorithms like Dijkstra’s algorithm, where we want the priority queue to always provide the pair with the smallest distance at the top.
- By default,
How It Works in Context
In Dijkstra’s algorithm, we typically use priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq; because:
- Min-Heap Behavior: The smallest distance vertex (or node) is always at the top of the priority queue.
- Efficient Access: Each time we need to process the next closest node, we can simply
popthe top of the queue. - Pair Structure: The
pair<int, int>structure allows each entry to store both the distance (first element) and node identifier (second element), enabling efficient management of distances for each node.
Example Usage
Assume we push pairs into this priority queue as (distance, node). If we insert pairs like (10, 1), (5, 2), and (15, 3), the queue will order them based on distance, with (5, 2) at the top.
#include <iostream>
#include <vector>
#include <queue>
#include <limits>
using namespace std;
const int V = 9; // Number of vertices in the graph
const int INF = numeric_limits<int>::max(); // Define infinity as the maximum int value
// A utility function to print the distance array
void printSolution(const vector<int>& dist) {
cout << "Vertex \t Distance from Source\n";
for (int i = 0; i < V; i++) {
cout << i << " \t\t " << dist[i] << "\n";
}
}
// Function to implement Dijkstra's algorithm using a priority queue
void dijkstra(const vector<vector<int>>& graph, int src) {
// Initialize distances from src to all other vertices as infinite
vector<int> dist(V, INF);
dist[src] = 0;
// Priority queue to select the vertex with the minimum distance
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, src}); // Push the source with a distance of 0
// While there are vertices in the priority queue
while (!pq.empty()) {
int u = pq.top().second;
pq.pop();
// Update distance values of adjacent vertices of the dequeued vertex
for (int v = 0; v < V; v++) {
// Only consider vertices that are reachable and not yet finalized
if (graph[u][v] && dist[u] != INF && dist[u] + graph[u][v] < dist[v]) {
dist[v] = dist[u] + graph[u][v];
pq.push({dist[v], v}); // Push updated distance to the queue
}
}
}
// Print the calculated shortest distances
printSolution(dist);
}
// Driver code
int main() {
// Example graph represented as an adjacency matrix
vector<vector<int>> graph = {
{ 0, 4, 0, 0, 0, 0, 0, 8, 0 },
{ 4, 0, 8, 0, 0, 0, 0, 11, 0 },
{ 0, 8, 0, 7, 0, 4, 0, 0, 2 },
{ 0, 0, 7, 0, 9, 14, 0, 0, 0 },
{ 0, 0, 0, 9, 0, 10, 0, 0, 0 },
{ 0, 0, 4, 14, 10, 0, 2, 0, 0 },
{ 0, 0, 0, 0, 0, 2, 0, 1, 6 },
{ 8, 11, 0, 0, 0, 0, 1, 0, 7 },
{ 0, 0, 2, 0, 0, 0, 6, 7, 0 }
};
// Execute Dijkstra's algorithm from source vertex 0
dijkstra(graph, 0);
return 0;
}